Rabu, 05 Januari 2011

'DIMENSI TIGA'

DIMENSI TIGA

DEFINISI, AKSIOMA DAN DALIL

Pengertian tentang Definisi, Aksioma dan Dalil :

1. Sifat-sifat yang dikemukakan untuk memperkenalkan nama sesuatu dalam pembicaraan tentang geometri disebut Definisi /Batasan.

2. Aksioma adalah pendapat yang dijadikan pedoman dasar dan merupakan Dalil Pemula, sehingga kebenarannya tidak perlu dibuktikan lagi, atau

Aksioma yaitu suatu pernyataan yang diterima sebagai kebenaran dan bersifat umum, tanpa memerlukan pembuktian.

Beberapa aksioma yang diperlukan dalam geometri ruang dikemukakan oleh EUKLIDES.

3. Dalil, (kaidah atau teorema) adalah kebenaran yang diturunkan dari aksioma, sehingga kebenarannya perlu dibuktikan terlebih dahulu.

AKSIOMA-AKSIOMA :

1. Melalui dua titik sembarang hanya dapat dibuat sebuah garis lurus.

2. Jika sebuah garis dan sebuah bidang mempunyai dua titik persekutuan, maka garis itu seluruhnya terletak pada bidang.

3. Melalui tiga buah titik sembarang hanya dapat dibuat sebuah bidang.

4. Melalui sebuah titik yang berada di luar sebuah garis tertentu, hanya dapat dibuat sebuah garis yang sejAjar dengan garis tertentu tersebut.

DALIL-DALIL :

A. Dalil untuk menentukan bidang :

1. Sebuah bidang ditemukan oleh tiga titik sembarang.

2. Sebuah bidang ditentukan oleh sebuah garis dan sebuah titik(titik berada diluar garis).

3. Sebuah bidang ditentukan oleh dua buah garis berpotongan.

4. Sebuah bidang ditentukan oleh dua buah garis sejajar.

Dimensi matematika

Dalam matematika, tidak ada satu pun definisi yang mencukupi untuk menyatakan konsep dalam segala situasi yang digunakan. Konsekuensinya, matematikawan membagi sejumlah definisi dimensi ke dalam tipe-tipe yang berbeda. Semuanya didasarkan pada konsep dimensi Euclides beruang-n, Eⁿ.

Titik E⁰ adalah dimensi-0,
Garis E E¹ adalah dimensi-1,
Bidang E² adalah dimensi-2,

dan secara rampat, Eⁿ adalah dimensi-n.

Senin, 06 Desember 2010

LOGIKA MATEMATIKA

A. Pernyataan

Yang dimaksud dengan kalimat atau pernyataan adalah kalimat yang mempunyai nilai benar atau salah, tetapi tidak sekaligus benar dan salah.

Ada dua jenis kalimat matematika, yaitu :

Kalimat tertutup, merupakan pernyataan yang nilai kebenarannya sudah pasti.

Contoh :

a) 3 x 4 = 12 (pernyataan tertutup yang benar)

b) 3 + 4 = 12 (pernyataan tertutup yang salah)

Kalimat terbuka, merupakan pernyataan yang kebenarannya belum pasti.

Contoh :

a : Ada daun yang berwarna hijau

b : Gula putih rasanya manis

B. Ingkaran Pernyataan

Ingkaran atau negasi suatu pernyataan adalah pernyataan yang menyangkal pernyataan yang diberikan. Ingkaran suatu pernyataan dapat dibentuk dengan menambah “Tidak benar bahwa ...” di depan pernyataan yang diingkar. Ingkaran pernyataan adalah ~ p.

Contoh :

Misalkan pernyataan p : Tembakau yang mengandung nikotin.

Ingkaran penyataan p adalah ~ p. Tidak benar bahwa tembakau mengandung nikotin.

Tabel kebenaran dari ingkaran

C. Pernyataan Majemuk

(i) Konjungsi

Pernyataan p dengan q dapat digabung dengan kata hubung logika “dan” sehingga membentuk pernyataan majemuk “p dan q” yang disebut konjungsi. Konjungsi “p dan q” dilambangkan dengan

(ii) Disjungsi

Pernyataan p dengan q dapat digabung dengan kata hubung logika “atau” sehingga membentuk pernyataan majemuk “p atau q” yang disebut disjungsi. Disjungsi p atau q dilambangkan dengan

(iii) Implikasi
Implikasi “jika p maka q” dilambangkan dengan

(iv) Biimplikasi

Biimplikasi “p jika dan hanya jika q” dilambangkan dengan

D. Ekuivalensi Pernyataan – Pernyataan Majemuk

E. Konvers, Invers, dan Kontraposisi

Dari sebuah implikasi dapat diturunkan pernyataan yang disebut konvers, invers dan kontraposisi dari implikasi tersebut.

TRIGONOMETRI

A. Pengertian Trigonometri

Trigonometri terdiri dari sinus (sin), cosinus (cos), tangens ( tan), cotangens (cot), secan (sec) dan cosecan (cosec). Trigonometri merupakan nilai perbandingan yang didefinisikan pada koordinat kartesius atau segitiga siku-siku.
Jika trigonometri didefinisikan dalam segitiga siku-siku, maka definisinya adalah sebagai berikut:

B. Nilai Trigonometri untuk Sudut-sudut Istimewa

C. Rumus-rumus Identitas Trigonometri

D. Rumus- Rumus Trigonometri

Aturan Trigonometri dalam Segitiga

LOGARITMA

Logaritma adalah operasi matematika yang merupakan kebalikan dari eksponen atau pemangkatan.

Rumus dasar logaritma:

b^c= a ditulis sebagai ^blog a = c (b disebut basis)

Beberapa orang menuliskan ^blog a = c sebagai log_ba = c.

I. Sifat-sifat Logaritma

a. Sifat Perkalian Logaritma

Perkalian logaritma samadengan penjumlahan logaritma dengan basis tetap.

b.Sifat Pembagian Logaritma

Jika hasil logaritma merupakan pembagian,hasilnya dapat diuraikan menjadi operasi pengurangan bilangan logaritma dengan basis tetap.

c. Sifat Perpangkatan Logaritma

Hasil operasi berupa bilangan logaritma berpangkat, dapat diuraikan

d. Sifat Penarikan Akar

Jika ada hasil operasi logaritma yang berbentuk akar, ubahlah terlebih dahulu menjadi bentuk pangkat untuk mempermudah penyelesaianya.

Beberapa Sifat Logaritma yang lain:

II. Persamaan Logaritma

III. Pertidaksamaan Logaritma

EKSPONEN

Eksponen adalah perkalian yang diulang-ulang. Orang menulis eksponen dengan indeks di atas, yang akan terlihat sebagai berikut:

x y

. Terkadang hal itu tak mungkin. Kemudian orang menulis eksponen menggunakan tanda ^: 2^3 berarti

23

Bilangan

x

disebut bilangan pokok, dan bilangan

y

disebut eksponen. Sebagai contoh, pada

23

, 2 adalah bilangan pokok dan 3 eksponen.

Untuk menghitung

23

seseorang harus mengalikan 3 kali terhadap angka 2. Sehingga $2^3=2 \cdot 2 \cdot 2$ . Hasilnya adalah $2 \cdot 2 \cdot 2=8$ . Apa yang dikatakan persamaan bisa juga dikatakan dengan cara ini: 2 pangkat 3 sama dengan 8.

Contoh:

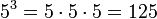
$5^3=5\cdot{} 5\cdot{} 5=125$
$x^2=x\cdot{} x$
$1 x = 1$ untuk setiap bilangan x

Jika eksponen sama dengan 2, maka disebut persegi karena area persegi dihitung menggunakan

a 2

. Sehingga

x 2

adalah persegi dari

x

Jika eksponen sama dengan 3, maka disebut kubik karena volume kubus dihitung dengan

a 3

. Sehingga

x 3

adalah kubik

x

Jika eksponen sama dengan -1 orang harus menghitung inversi bilangan pokok. Sehingga: $x^{-1}=\frac{1}{x}$ Jika eksponen adalah integral dan kurang dari 0, orang harus membalik bilangan dan menghitung pangkat. Sebagai contoh:

$2^{-3}=(\frac{1}{2})^3=\frac{1}{8}$

Jika eksponen sama dengan $\frac{1}{2}$ hasilnya adalah akar persegi bilangan pokok. Sehingga $x^{\frac{1}{2}}=\sqrt{x}.$ Contoh:

$4^{\frac{1}{2}}=\sqrt{4}=2$

Dengan cara yang sama, jika eksponen $\frac{1}{n}$ hasilnya adalah akar ke-n, sehingga:

$a^{\frac{1}{n}}=\sqrt[n]{a}$

Jika eksponen merupakan bilangan rasional $\frac{p}{q}$ , hasilnya adalah akar ke-q bilangan pokok yang dipangkatkan p, sehingga:

$a^{\frac{p}{q}}=\sqrt[q]{a^p}$

Eksponen bisa juga tak rasional. Untuk menjadikan bilangan pokok a menjadi pangkat ke-x yang tak rasional, kita menggunakan rangkaian ketidakterhinggaan bilangan rasional (x_i), yang limitnya adalah x:

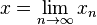
$x=\lim_{n\to\infty}x_n$

seperti ini: $a^x=\lim_{n\to\infty}a^{x_n}$

Ada beberapa aturan yang membantu menghitung pangkat:

$\left(a\cdot b\right)^n = a^n\cdot{}b^n$
$\left(\frac{a}{b}\right)^n = \frac{a^n}{b^n},\quad b\neq 0$
$a^r \cdot{} a^s = a^{r+s}$
$\frac{a^r}{a^s} = a^{r-s},\quad a\neq 0$
$a^{-n} = \frac{1}{a^n},\quad a\neq 0$
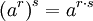
$\left(a^r\right)^s = a^{r\cdot s}$
$a^0 = 1,\quad a\neq 0$ : Bila bilangan pokok lebih besar daripada 1 dan eksponen 0, jawabannya 1. Jika bilangan pokok dan pangkat sama dengan 0, jawabannya tak terdefinisikan.

Ekponen matriks bisa pula dihitung. Matriks itu harus persegi. Sebagai contoh: $I^2=I \cdot I=I$ .